D.1 Stellar Quantities

Objects in the universe

Stellar Clusters: groupings of large numbers of stars that attract each other gravitationally and are relatively close to one another

• Open cluster: contain old stars
• Globular cluster: contain younger stars

Constellation: A group of stars in a recongnisable pattern that appear to be near each other in space.

Difference between stellar cluster and constellation：Star clusters are groups of stars that are ‘connected’ by a significant gravitational force ands move around tougher as the galaxy rotates. A constellation is a group of stars that appear to be related simply because of the angle of view on Earth.

The nature of stars

The stability of a star depends on the equilibrium between radiation pressure and gravitational pressure

• Radiation pressure make the star expand
  • Nuclear fusion provides the energy the star needs to keep it hot so that the star’s radiation pressure is high enough to oppose gravitational contraction.
• Gravitation make the star collapse

Proton–proton cycle (fusion reactions)

• $^1_1\text H+^1_1\text H\rightarrow^2_1\text H+^0_1e^++v_e$
• $^2_1\text H+^1_1\text H\rightarrow^3_2\text He+\gamma$
• $^3_2\text He+ ^3_2\text He\rightarrow^4_2\text He+2^1_1\text H$

Astronomical distances

Light year (Ly) & Astronimical unit (AU)

• A Light year is the distance travelled by light in one year, which is $9.46×10^{15}m$

• An Astronimical unit is the average radius of the Earth’s orbit around the Sun, which 1AU = $1.5×10^{11}m$ = 3.26 ly

Stellar parallax and its limitations

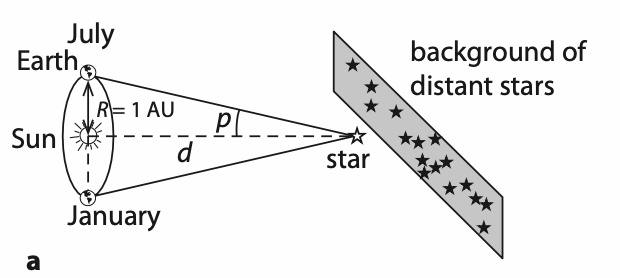
When an object is observed at two difference potitions, it appears displaced relative to a fixed background.

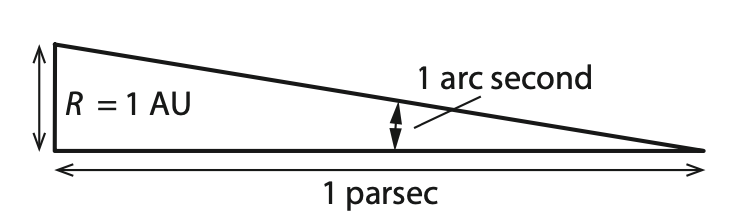
The parallax angle is the angle, at the position of the star, that is subtended by a distance equal to the radius of the Earth’s orbit around the Sun (1AU).

A parsec is the distance to a star whose parallax is 1 arc second, which is 3.09×10^16^m

An arc second is 1/3600 of a degree

• The average distance between stars in a galaxy is about 1pc
• Obveratory on Earth could see star within 100pc by the method of parallax (Because of the distortion caused by atmosphere and uncertainty of the facility)
• High resolution satellite could see star within 100,000pc
• Distance toward the edge of milky way galaxy is 30,000pc
  • Galaxy cluster (30 galaxies): 1,000,000pc

The parallax method is also a means of measuring astronomical distances:

$$ d \textcolor{grey}{\text{ (parsecs)}}=\frac{1}{p\textcolor{grey}{\text{ (arc seconds)}}} $$

But if the star is too far, p would be too small to be measured accureately!

Apparent brightness & Luminosity

Apparent brightness: The received power per unit area $$ b=\frac{L}{4\pi d^2} $$

• $b$: Apparent brightness ($Wm^{-2}$)

• $L$: Luminosity ($W$)

• $d$: Distance ($m$)

• Apparent brightness is easily measured by charge-coupled device (CCD).

Luminosity: Total power radiated by the star (W)

$$ L=\sigma AT^4 $$

• $\sigma$: Stefan-Boltzmann constant

• $A$: Area of the star ($m^2$)

• $T$: Temperature ($K$)

A star is assumed to radiate like a black body.

$L_{\bigodot}$ symbolized the luminosity of the sun, the same for other variables.