3. Thermal physics

3.1 Thermal concepts

Temperature and absolute temperature

There have two commonly used measurment of temperature, one is Celsius(摄氏度) and the other one is Kelvin（开氏度） The temperature difference between them is same ${\Delta K}={\Delta C}$ Absolute zero is 0K whcih is -273$\Celius$

Heat (Internal Energy)

• Heat is energy that is transferred from one body to another as a result of a difference in temperature.
• Internal energy is the total random kinetic energy of the particles of a substance, plus the total inter-particle potential energy of the particles.
• The heat (temperature) is the only determintion of the kenetic energy (温度是衡量动能的唯一标准)

Specific heat capacity

Specific heat capacity follow the formula: $$Q=mc{\Delta T}$$ Q is energy(heat), m is mass, ${\Delta T}$ is Temperature change and c is specific heat capacity.

• To define this equation, it means that suppose there's a object A have specific heat capacity c and it required Q energy to raise it's temperature 1K(C)
• Different substances have different specific heat capacities because of different physical properties

Change of phase

When heating some substances it might not necessarily increase temperature but change phase

• melting (solid to liquid)
• freezing (liquid to solid)
• vaporisation/boiling (liquid to gas)
• condensation (gas to liquid)
• Sublimation（solid to gas）
• condensation (gas to solid)

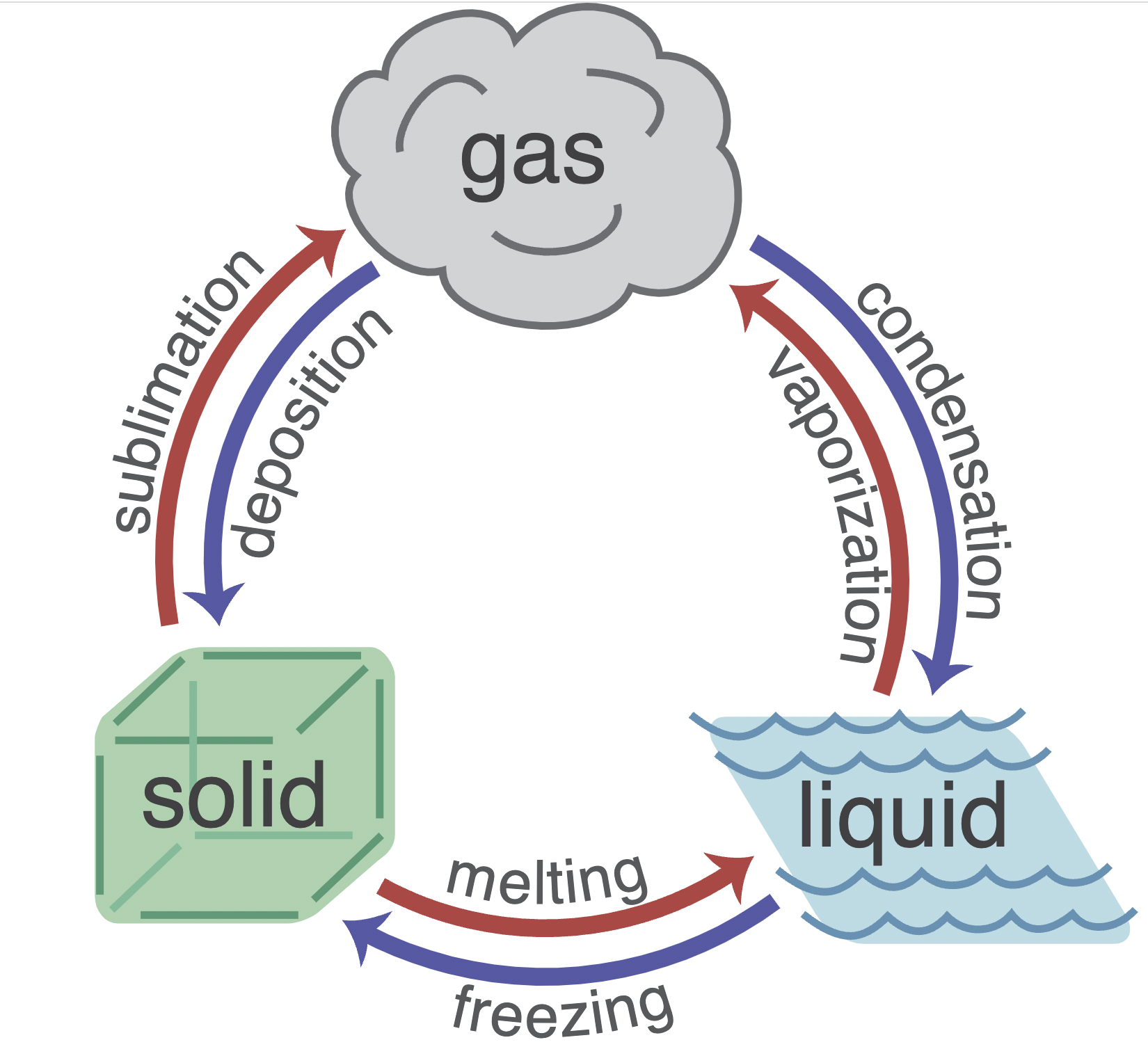
Specific latent heat

Specific latent heat follow the formula: $$Q = mL$$ In this case the L can be replaced by $L_V$ (vaporisation) and $L_F$ (fusion)

• specific latent heat of fusion: The amount of heat required to change mkg of a substance from solid to liquid without any change in temperature.
• Specific latent heat of vaporization: The amount of heat required to change mkg of a substance from liquid to gas without any change in temperature.

3.2 Modelling a gas

The Avogadro constant

Avogadro constant $N_A$ is a experimental constant that measurment the number of particle in one mole of substance, which $N_A=6.022\times 10^{23}mol^{-1}$ mole is measured by the amnount of particle carried by 12g of Carbon-12 which repersent as $n$ $$n={\frac{N}{N_A}}$$ Where $n$ is mol number, $N$ is number of particle and $N_A$ is avogadro constnt

Pressure

Pressure is defined as the normal force applied per unit area which followed the equation: $$p={\frac{F}{A}}$$ Where $p$ is pressure $F$ is force and $A$ is area.

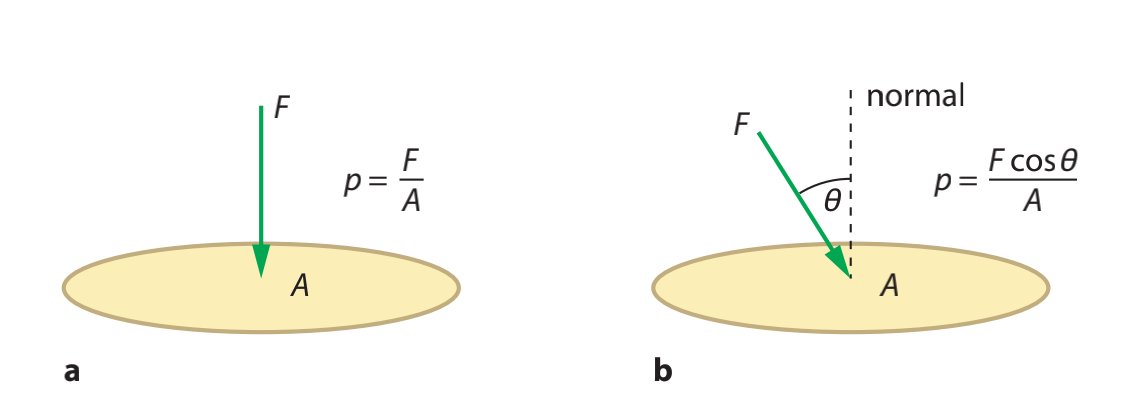
If the force dose not vertically acting at an object, then should use the equation: $$p=\frac{Fcosθ}{A}$$ p in non-closed condition should be equal to 1atm which is $1.013 × 10^{5}Pa$ on Earth

Ideal gas

An ideal gas is a theoretical model of a gas which should follow the rules that:

• The molecules are point particles, each with negligible volume.
• The molecules obey the laws of mechanics.
• There are no forces between the molecules except when the molecules collide.
• The duration of a collision is negligible compared to the time between collisions.
• The collisions of the molecules with each other and with the container walls are elastic.
• Molecules have a range of speeds and move randomly.

The real gas at high temperature and low pressure will close to ideal gas

An ideal gas should followed the equation: $$PV=nRT$$ P is pressure, V is volume, n is mole number, R is ideal gas constant ($8.31Jmol^{-1}K^{-1}$) and T is temperature

The Boltzmann equation

$$E_{avg}=\frac{3}{2}k_bT$$ This is measurment of average kenetic energy in ideal gas, and $k_b$ means $\frac{R}{N_A}$ which is $1.38\times10^{−23}JK^{−1}$.

Therefore the average internal energy would be: $$U=\frac{3}{2}pV$$