Skip to main content

3. Thermal physics

![booklet_3.png](/physics/booklet_3.png)
Gobooklet_3.png

to questionbank: https://library.tis.wiki/QuestionBank/questionbank.ibo.org/en/teachers/00000/questionbanks/46-dp-physics/syllabus_sections/2598.html
#

3.1 Thermal concepts
##

Temperature and absolute temperature

There have two commonly used measurment of temperature, one is **Celsius(摄氏度)** and the other one is **Kelvin（开氏度）**
 The **temperature difference**difference between them is **same**same ${\Delta K}={\Delta C}$
Absolute zero is 0K whcih is -273C273$\Celius$

##

Heat Heat((Internal Energy)
>**Heat**

  • Heat is energy that is **transferred**transferred from one body to another as a
    result of a **difference in temperature**temperature.

    • >**

  • Internal energy**energy is the **total**total random **kinetic energy**energy of the
    particles of a substance, **plus**plus the total inter-particle **potential
    energy**energy     of the particles.


    • >

  • The **heat**heat (temperature) is the **only**only determintion of the **kenetic energy**energy (温度是衡量动能的唯一标准)

##  specific

Specific heat capacity


**

Specific heat**heat capacity follow the formula:
$$Q=mc{\Delta T}$$
Q is energy(heat), m is mass, ${\Delta T}$ is Temperature change and c is specific heat capacity.

-

  • To define this equation, it means that suppose there's a object A have specific heat capacity c and it required Q energy to raise it's temperature **1K(C)**

    -

  • Different substances have different specific heat capacities because of different physical properties
    ##

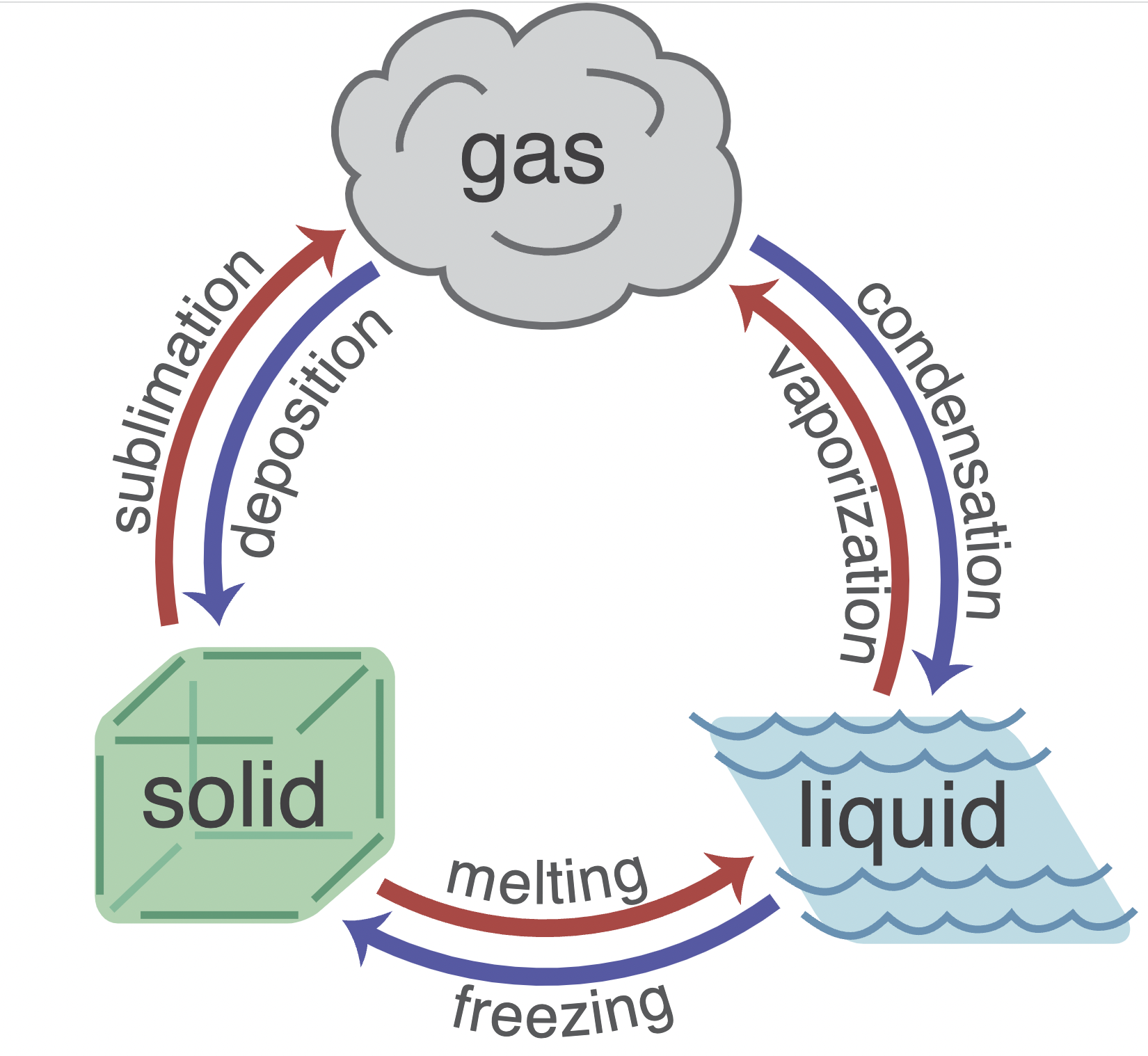
Change of phase

When heating some substances it might not necessarily increase temperature but change phase
-

melting(
  • melting (solid to liquid)
    -
    • freezing(
  • freezing (liquid to solid)
    -
  • vaporisation/boiling(boiling (liquid to gas)
    -
    • condensation(
  • condensation (gas to liquid)
    -
  • Sublimation（solid to gas）
    -
    • condensation(
  • condensation (gas to solid)
    ![phase_change.png](/physics/phase_change.png)

    ##phase_change.png

Specific latent heat

Specific latent heat follow the formula:
$$Q = mL$$
In this case the L can be replaced by L~V~$L_V$ (vaporisation) and L~F~$L_F$ (fusion)
-

  • specific latent heat of fusion: The amount of heat required to change **mkg**mkg of a substance from **solid**solid **to liquid**liquid without any change in temperature.
    -
  • Specific latent heat of vaporization: The amount of heat required to change **mkg**mkg of a substance from **liquid to gas**gas without any change in temperature.
    #

3.2Modelling2 Modelling a gas
##

The Avogadro constant

Avogadro constant $N_A$ is a **experimental constant**constant that measurment the number of particle in one **mole**mole of substance, which $N_A=6.022\times 10^{23}mol^{-1}$
mole is measured by the amnount of particle carried by 12g of Carbon-12 which repersent as $n$
$$n={\frac{N}{N_A}}$$
n Where $n$ is mol number, N$N$ is number of particle and $N_A$ is avogadro constnt
##

Pressure

Pressure is defined as the **normal force**force applied **per unit area**area which followed the equation:
$$p={\frac{F}{A}}$$
p Where $p$ is pressure F$F$ is force and A$A$ is area.
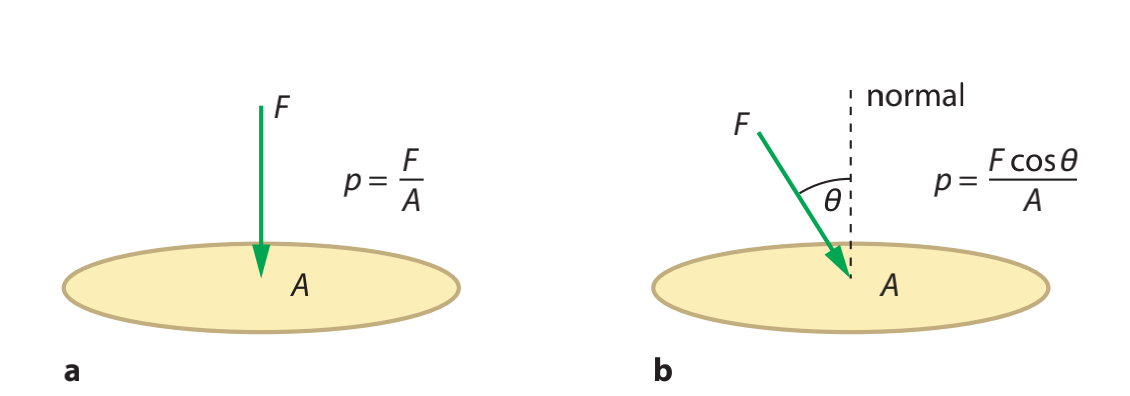
![pressure.png](/physics/pressure.png)
pressure.png

If the force dose **not vertically**vertically acting at an object, then should use the equation:
$$p=\frac{Fcosθ}{A}$$
p in **non-closed**closed condition should be equal to 1atm which is $1.013 × 10^{5}Pa$ on Earth
##

Ideal gas

An ideal gas is a theoretical model of a gas which should follow the rules that:
-

  • The molecules are **point particles**particles, each with **negligible volume**volume.
    -
  • The molecules obey the laws of mechanics.
    -
  • There are **no forces**forces between the molecules except when the molecules collide.
    -
  • The duration of a collision is **negligible**negligible compared to the time between collisions.
    -
  • The collisions of the molecules with each other and with the container walls are **elastic**elastic.
    -
  • Molecules have a **range of speeds**speeds and **move randomly**randomly.
    >

The real gas at high temperature and low pressure will close to ideal gas
{.is-info}


An ideal gas should followed the equation:
$$PV=nRT$$
P is pressure, V is volume, n is mole number, R is ideal gas constant(constant ($8.31Jmol^{-1}K^{-1}$) and T is temperature
##

The Boltzmann equation

$$E_{avg}=\frac{3}{2}k_bT$$
This is measurment of average kenetic energy in ideal gas, and $k_b$ means $\frac{R}{N_A}$ which is $1.38\times10^{−23}JK{JK^{−1}$
.

Therefore the average internal energy would bebe:
$$U=\frac{3}{2}pV$$

Back to top