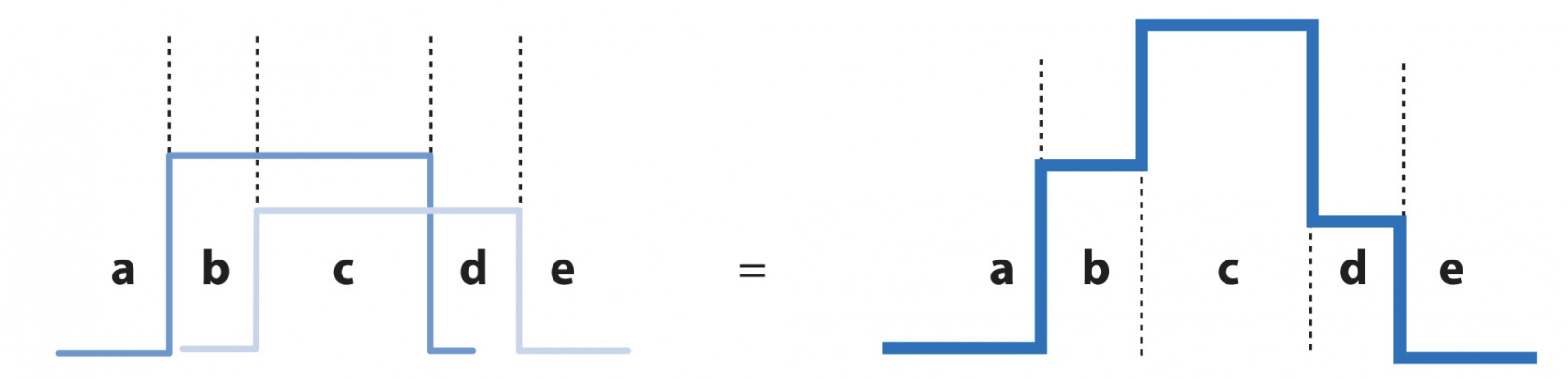Skip to main content

4. Waves

booklet_4.png

4.1 Oscillations

Oscillation and simple harmonic oscillations

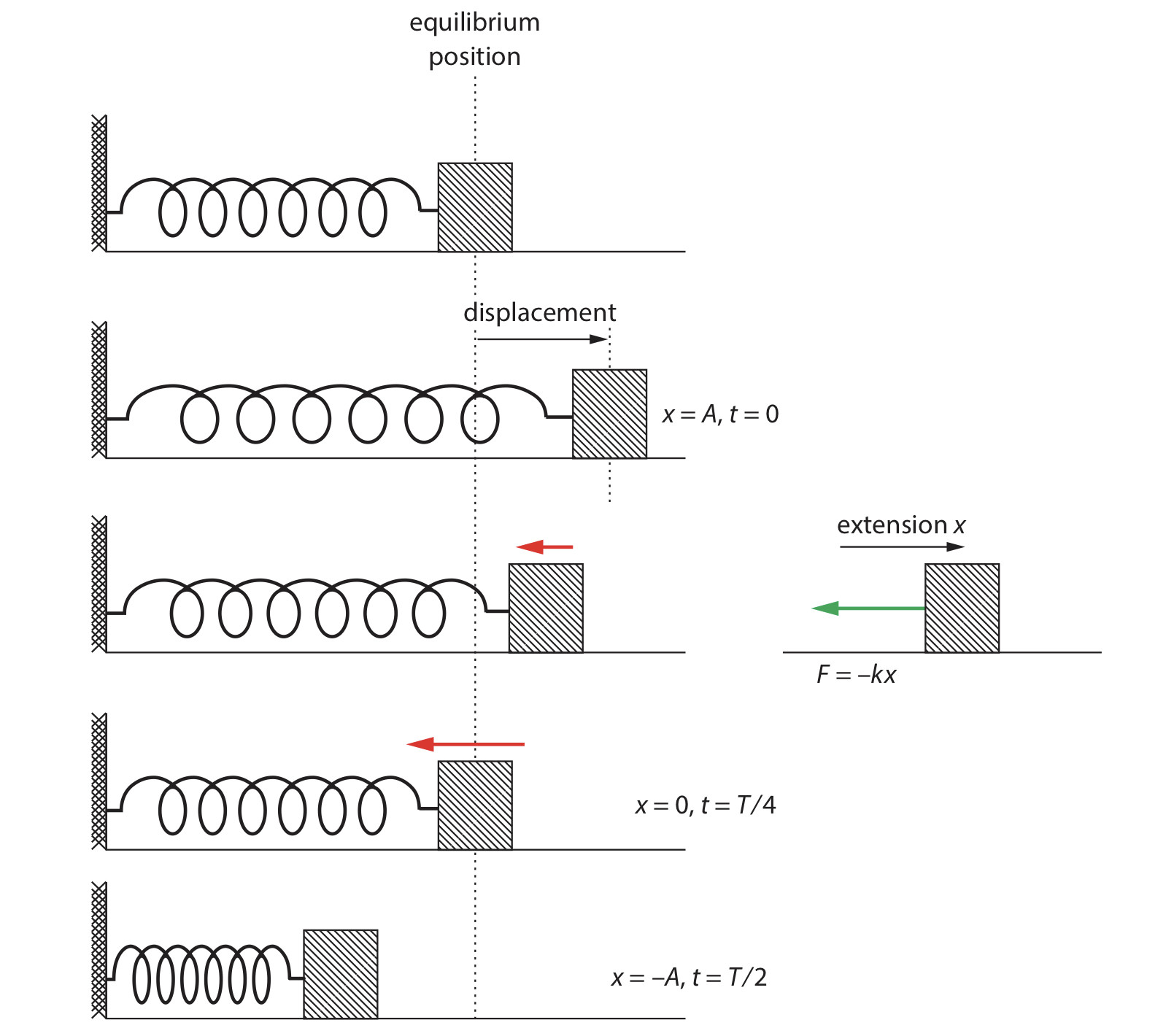
Oscillation

Oscillations are periodic motions which center around an equilibrium position and repeat the motion.

Period ($T$) means the time taken to complete one full oscillation. Amplitude measured the maximum displacement from the equilibrium.

Simple harmonic oscillations

Simple harmonic oscillations/Simple harmonic motion(SHM) is a special kinds of oscillation have several characteristics:

  • the period and amplitude are constant
  • the period is independent of the amliptude
  • the displacement, velocity and acceleration are sine or cosine functions of time.
  • $a∝-x$ shm_of_pendulum.jpeg shm_of_spring.jpeg

Frequency and phase difference

Frequency$(f)$ means the number of full oscillations per second, whcih followed the equation: $$f=\frac{1}{T}$$ In this case the T is period.

Phase difference$(φ)$ means the difference between two SHMs with the same frequency in terms of their relative position in a cycle measured in radian $$φ=\frac{shift}{T}\times 360°$$

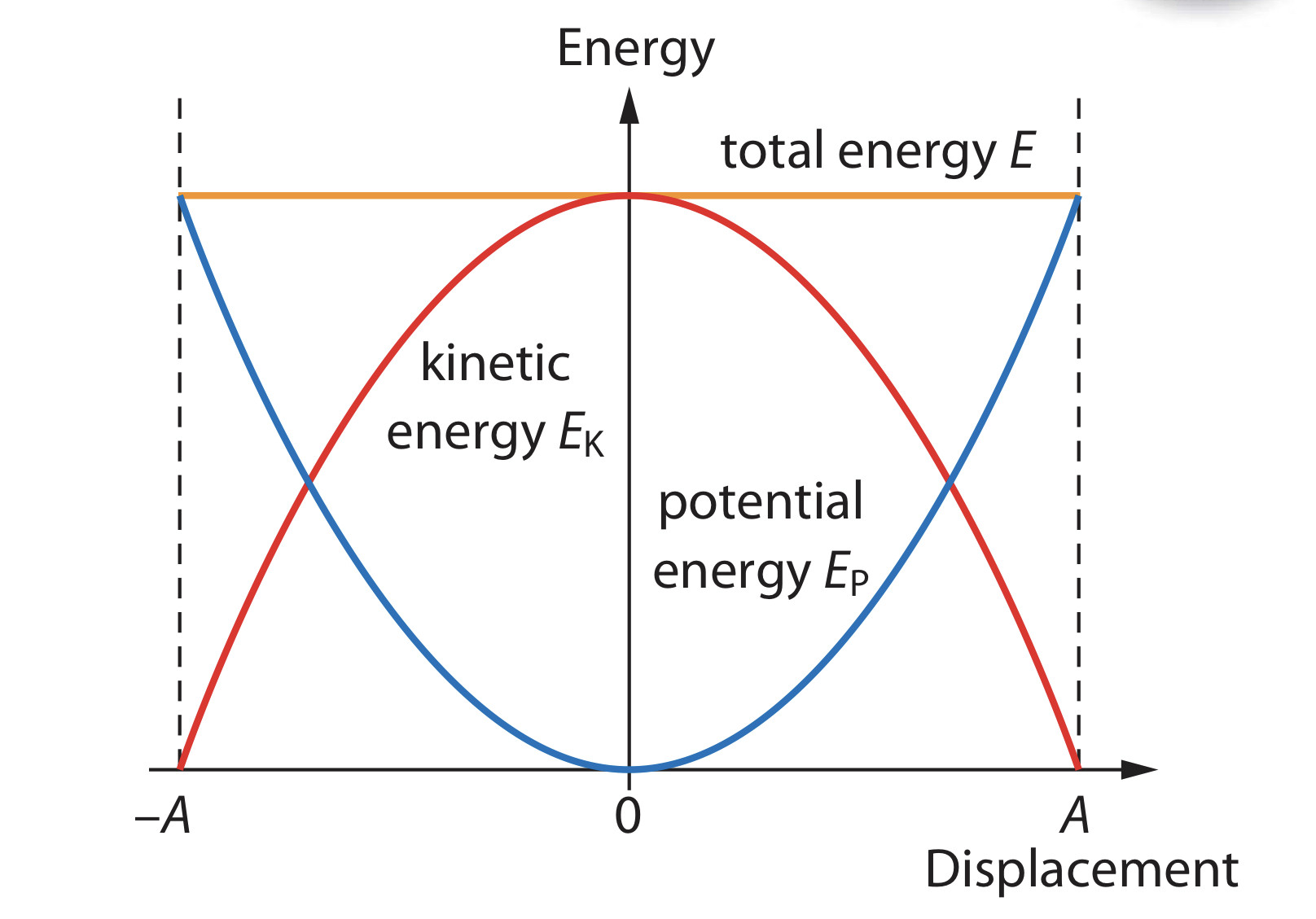
Energy in simple harmonic motion

The total energy of the system followed the equation: $$E_T=E_P+E_K=(E_K){max}=(E_p){max}$$ energy_in_shm.jpeg

4.2 Travelling waves

Wavelength and wave speed

Wavelength, frequency, and period follow the same rules of SHM.

Wave speed can be calculate by following equation: $$v=fλ$$ In this case, v is wave speed, f is frequency and λ(lambda) means wave length

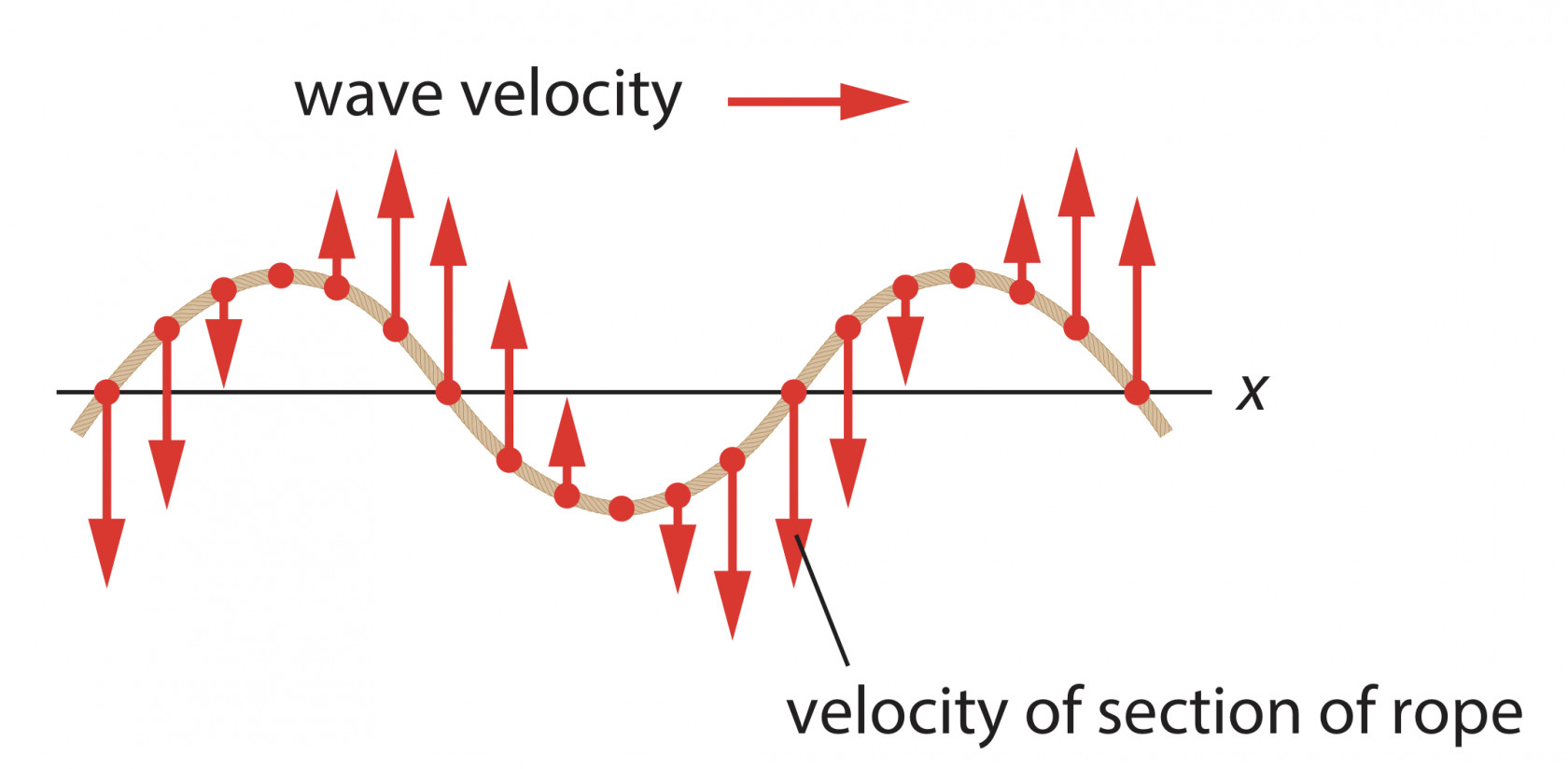
Longitudinal wave and Transverse wave

Transverse wave is the wave that direction of displacement and direction of energy transfer is at a right angle

  • A point with maximum positive displacement is called a crest.
  • A point with minimum displacement is called a trough. transverse_wave.jpeg

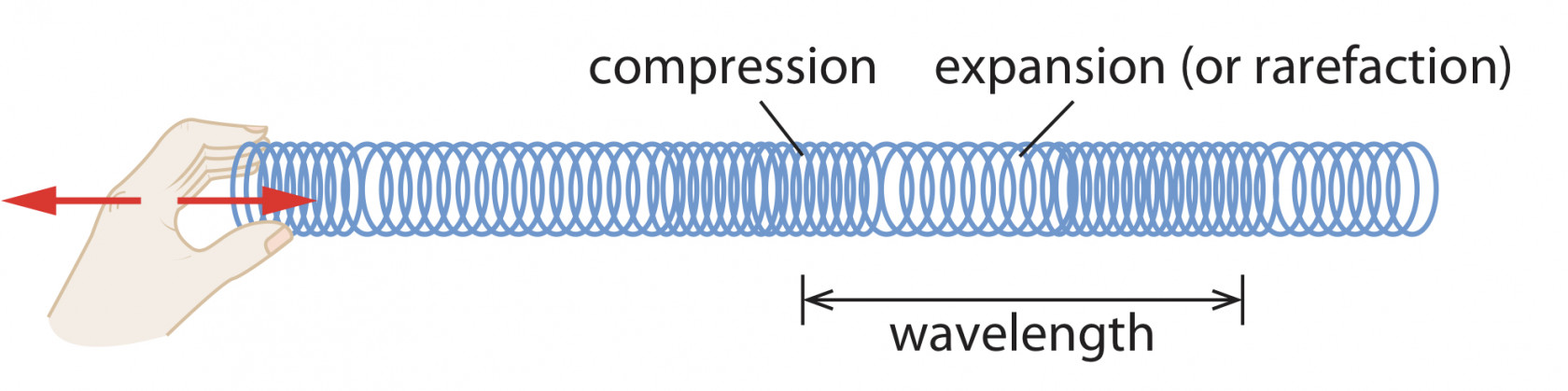
Longitudinal wave is the wave that direction of displacement and direction of energy transfer parallel

  • A region where particles are closed to each other is called a compression.
  • A region where particles are furthest apart from each other is called a rarefaction. longitudinal_waves.jpeg

4.3 Wave characteristics

Wavefronts and rays

Wavefront is a surface through crests and normal to the direction of energy treansfer of the wave

Ray is the lines in the direction of energy transfer of the wave

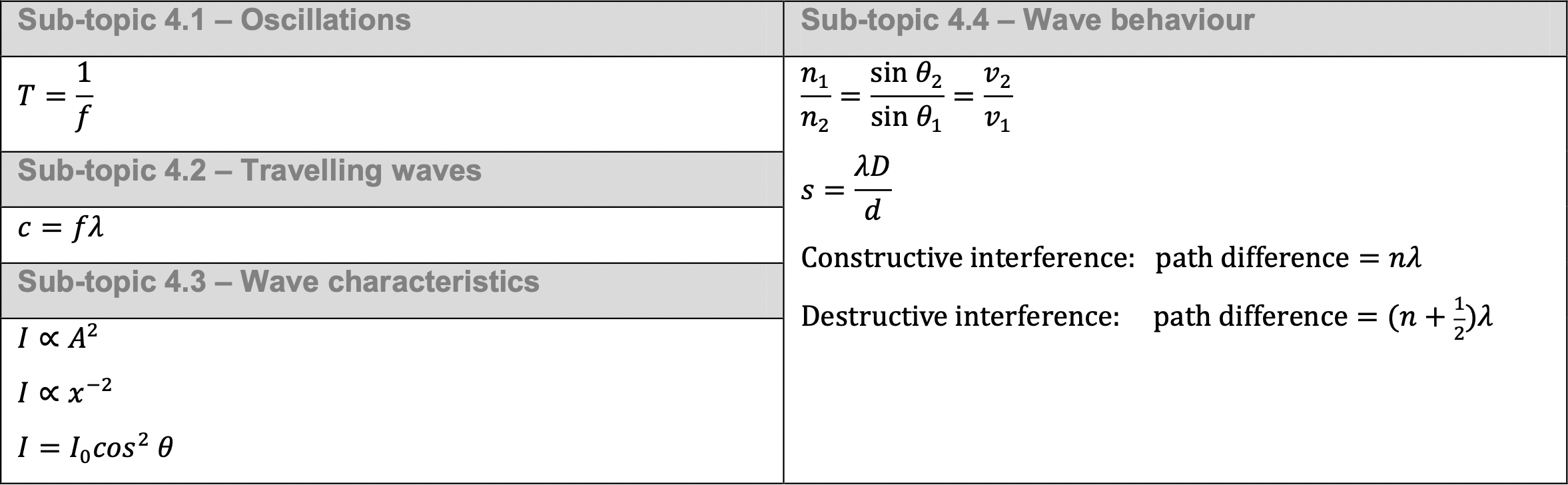
Amplitude and intensity

The amplitude and intensity of a wave depends on its energy.

The point source of power P radiates equally in all direction which follow the equation: $$I=\frac{P}{4{\pi}x^2}$$

The intensity of a wave is proportional to the square of its amplitude ($I∝A^2$).

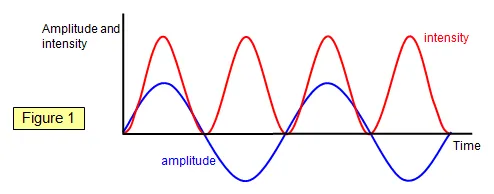
amplitude_and_intensity.webp

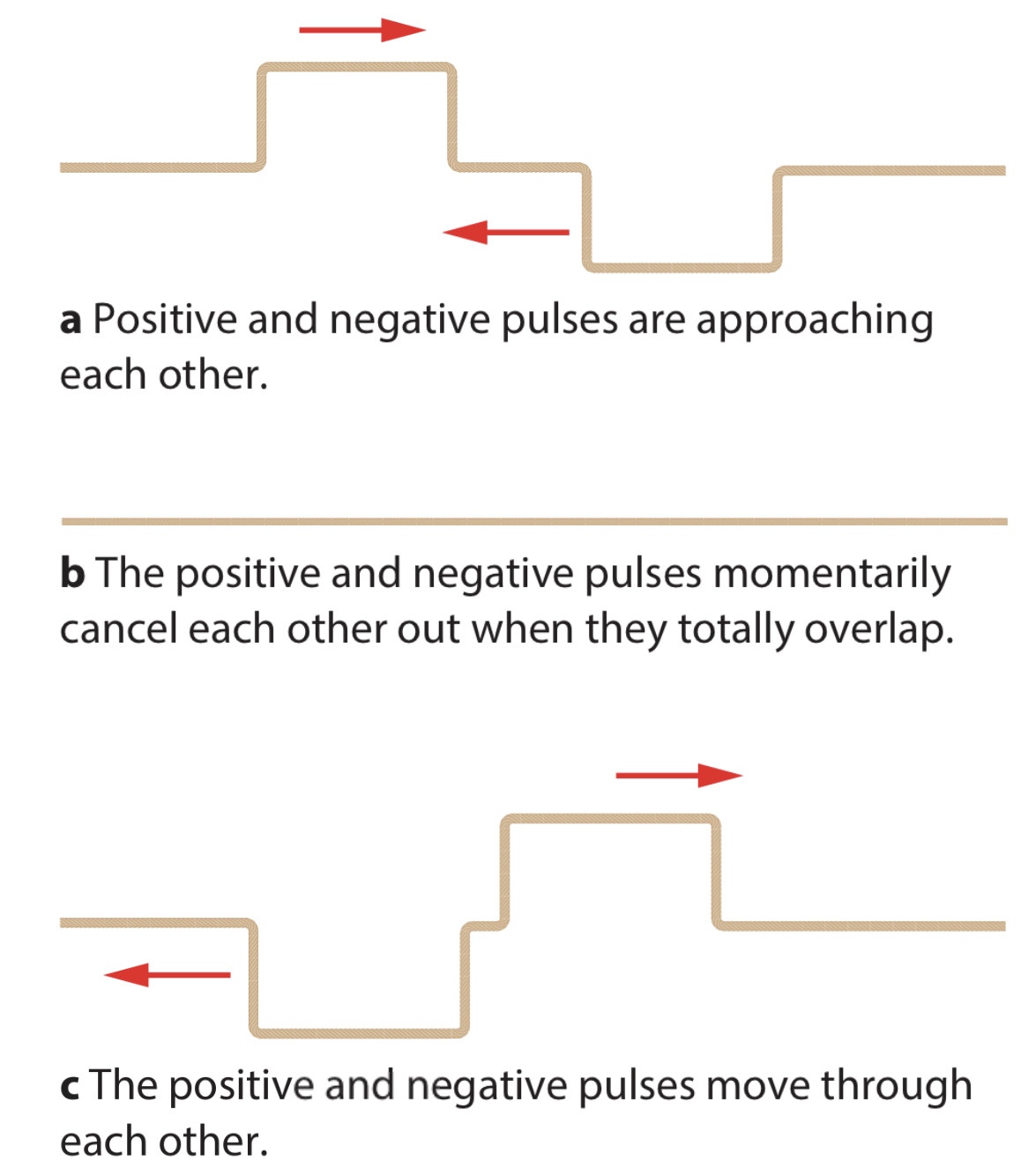
The principle of superposition

When two or more waves of the same type arrive at a same point in space at the same time, the displacement of the medium at that point is sum of those waves. For example:

wave_superpose.jpeg

The wave can also be negative such as: wave_phenomenom.jpeg

Polarization

Visible light can also treated as a wave

The polarization means that the orientation of the oscillation of light

Such as

As the graph shows, the left side is unpolarized light which orientation is in random direction but after the polarzation the light only left one orientation.

Malus's law

The malus's law follow the equation $$I=I_0cos^2θ$$ The $I$ is the after polarized intensity and $I_0$ means the incident intensity This equation shows that the difference between the incident intensity will be reduce if the polariser and the polarization light. If the degree is 0 will not have effect but if the degree is 90 then the $I$ will be zero. malus's_law.jpeg

Polarisation by reflection

  • When light pass through medium which have different refract index, part of the light been reflect but others been refracted.
  • The reflected light is partially polarized which the plane of polarisation is parallel to the reflecting surface.

polarisation_by_reflection.jpeg

4.4 Wave behaviour

Reflection

reflection.jpeg

The angle of incidence $i$ (angle between the ray and the normal to the reflecting surface at the point of incidence) is equal to the angle of reflection $r$ (angle between the normal and the reflected ray)

Snell's law

Snell's law give us equation: $$\frac{n_1}{n_2}=\frac{sinθ_2}{sinθ_1}=\frac{c_2}{c_1}$$ The n means different refractive index, and c means the light of speed in different medium. snell's_law.jpeg

Diffraction

Diffraction takes place when a wave with wavelength comparable to or larger than the size of an aperture or an obstacle moves through or past the aperture or obstacle moves through or past the aperture or obstacle

Single slit interference

single_slit_interference.jpeg

Double source interference

double_source_interference.jpeg When both have same sign of wavelength, then will happened a constructive interference, and if there has opposite sign of wavelength, then will have destructive interference followed the equation: Constructive interference:$nλ$ destructive interference:$(n+\frac{1}{2})λ$

Double-slit interference

The two slit will have different λ so there will be Constructive and destructive interference which reflect in graph is interlaced light and dark stripes and followed the equation: $$s=\frac{λD}{d}$$ double-slit_interference.jpeg

Standing wave

Standing wave is the superposition of two wave which is opposite

Standing waves on strings

The n shows the harmonic, and the graph shows the various of nth harmonic which reflect in graph standing_waves_on_strings.jpeg To sum up, the eqaution could be: $$λ_n=\frac{2L}{n}$$

Standing waves on pipe

There have different condition in pipe which is

  • Two close
  • Two free
  • One close and one free And can follow the equation: img_cf5333f0cbb2-1.jpeg
Back to top