2. Mechanics
Motion
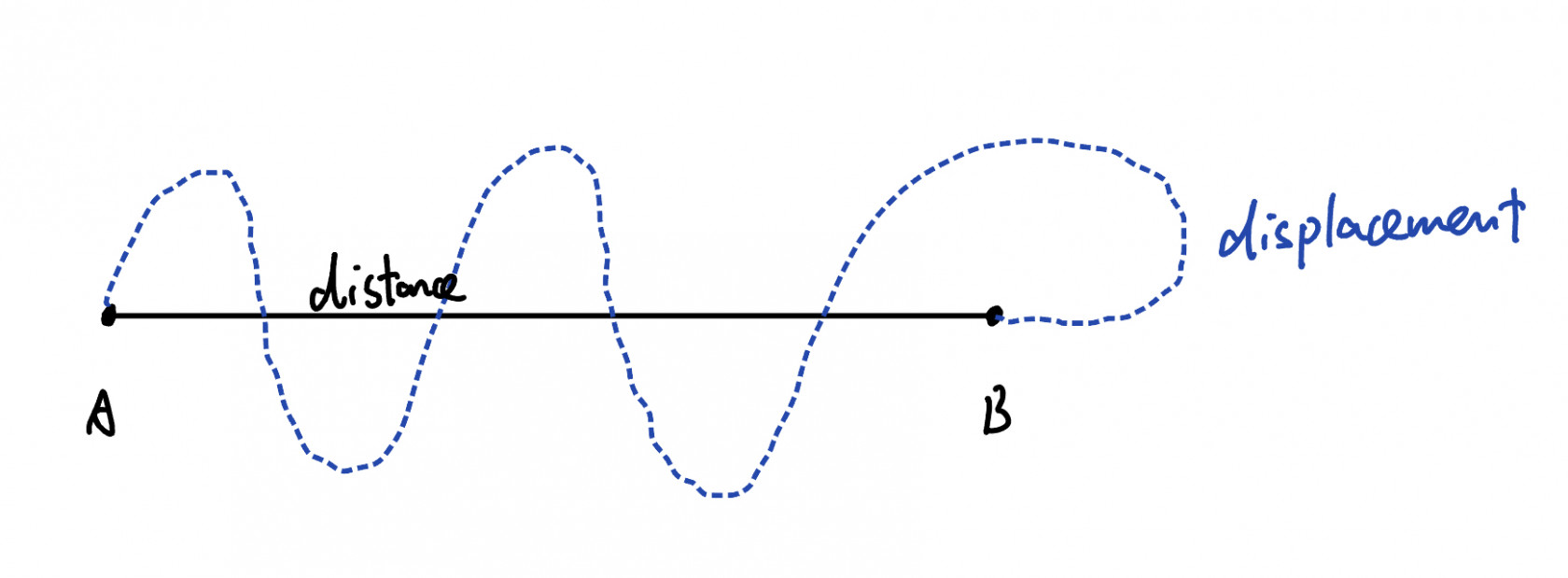
Distance and displacement
| Distane | Displacement |
|---|---|
| scalar | vector |
| The length of the shortest straight line between two different point | The distance moved from the initial position to the end point |
| |s| | s |
Speed and Velocity
| Speed | Velocity |
|---|---|
| Scalar | Vector |
| How fast an object moves/rate of change of distance to time | Speed with the direction/rate of change of displacement to time |
| |v| | v |
| The derivative of displacement is velocity |
Acceleration
- vector
- Describes how fast the speed of an object changes/The rate of change of velocity to time
- The derivative of velocity is acceleration
| Equations of motion for uniform acceleration |
|---|
| ${v}=ut+\frac{1}{2}at^2$ |
| ${s}=ut+\frac{1}{2}at^2$ |
| ${v^2}=u^2+2as$ |
| ${s}=\frac{(u+v)t}{2}$ |
| v=velocity, s=displacement, a=acceleration, t=time |
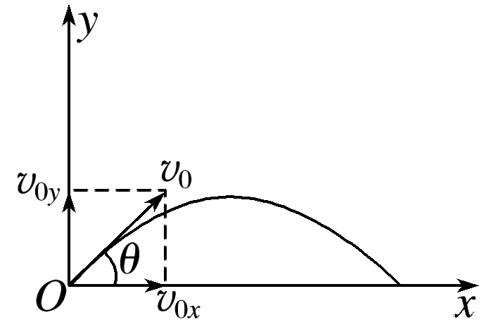
Projectile motion
Projectile motion is
The projectile motion is the uniform speed curve motion in which the object is launched from a certain initial angle, ignoring the air resistance, and the object is only affected by gravity (g) and initial velocity
- The air resistance is negligible
- The horizontal component of velocity is constant
- The verticle component of velocity has acceleration downward of g(9.81ms^-2)
- The motion's is zero when it at the heighest point
- The motion is symmetric
| The verticle and horizontal component |
| Horizontal component | Verticle component |
|---|---|
| u~x~ | u~y~ |
| v~x~=u~x~ | v~y~=u~y~ - gt |
| v~x~=ucosθ | v~y~=usinθ - gt |
Forces
different kinds of force
Forces and their direction {.tabset}
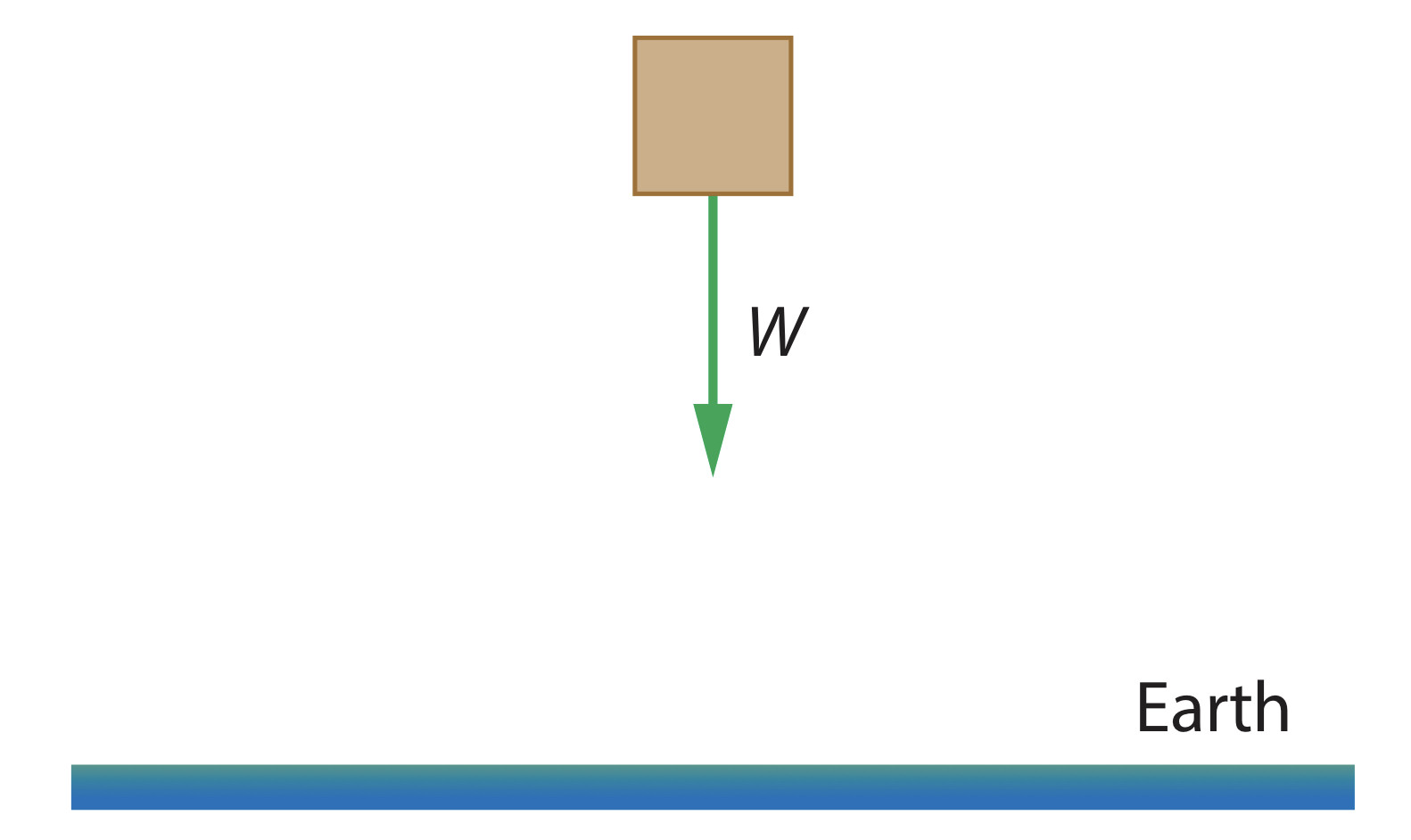
Weight
| Weight |
|---|
| ${W}=mg$ |
| Where W is weight, m is mass and g is gravity constant(9.81ms^-2^ on Earth) |
| The weight is measurement of gravitational attraction between the mass m of a body and the mass of the planet on which the body is placed |
 |
Tension
| Tension |
|---|
| When two forces are applied to the rope, it will tight up and have tension. PS. only the tight rope has tension |
 |
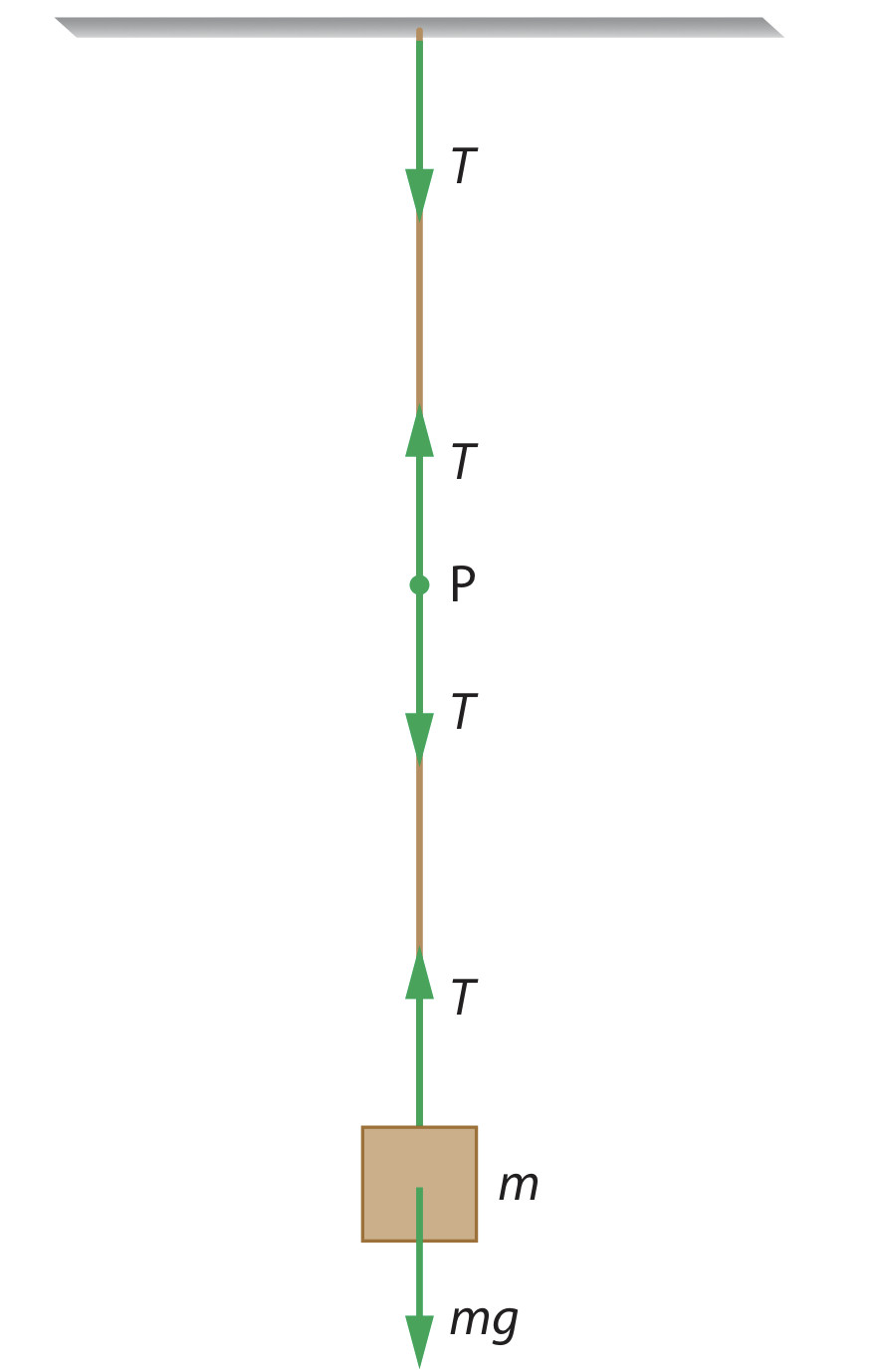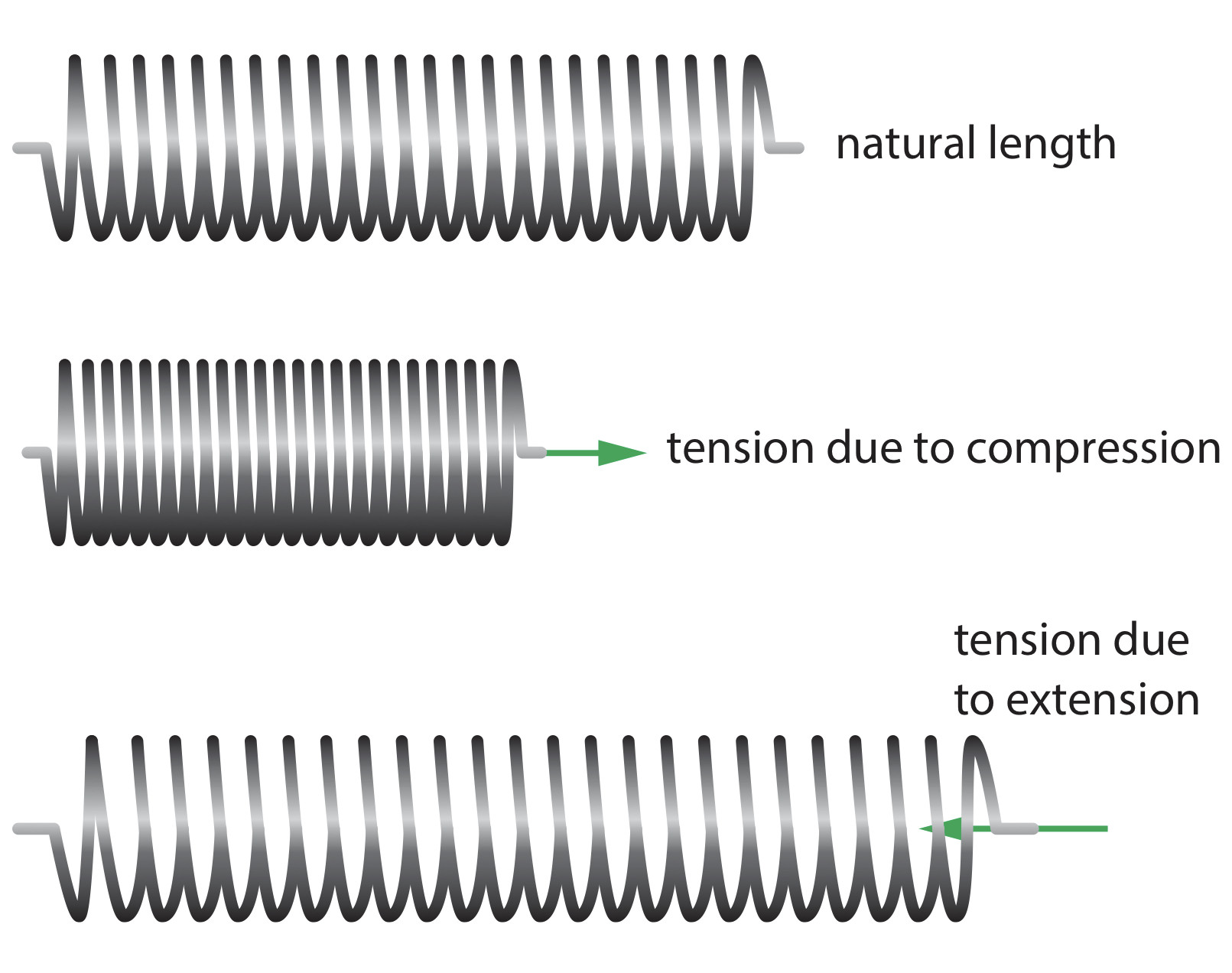
Forces in springs
| Forces in springs |
|---|
| ${T}=kx$ |
| Where T is spring force, k is spring constant and x is the displacement between the equilibrium point and release point |
| When there's displacement of spring, the spring will store the force and try to back to the original value |
 |
Drag forces
| Drag forces |
|---|
| Drag forces are forces that oppose the motion of a body through a fluid(gas or liquid) |
 |
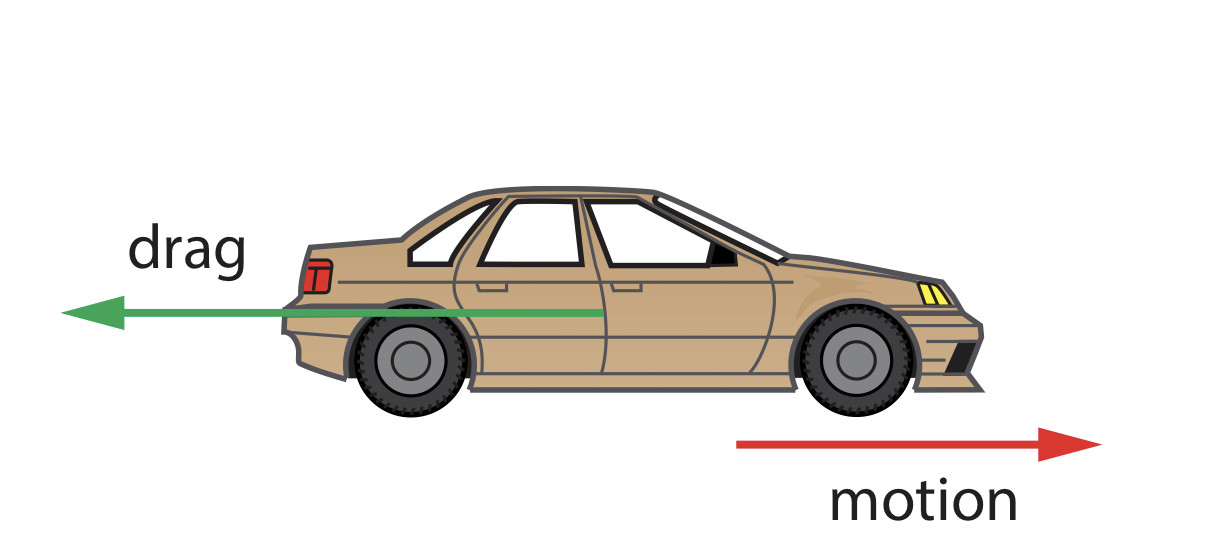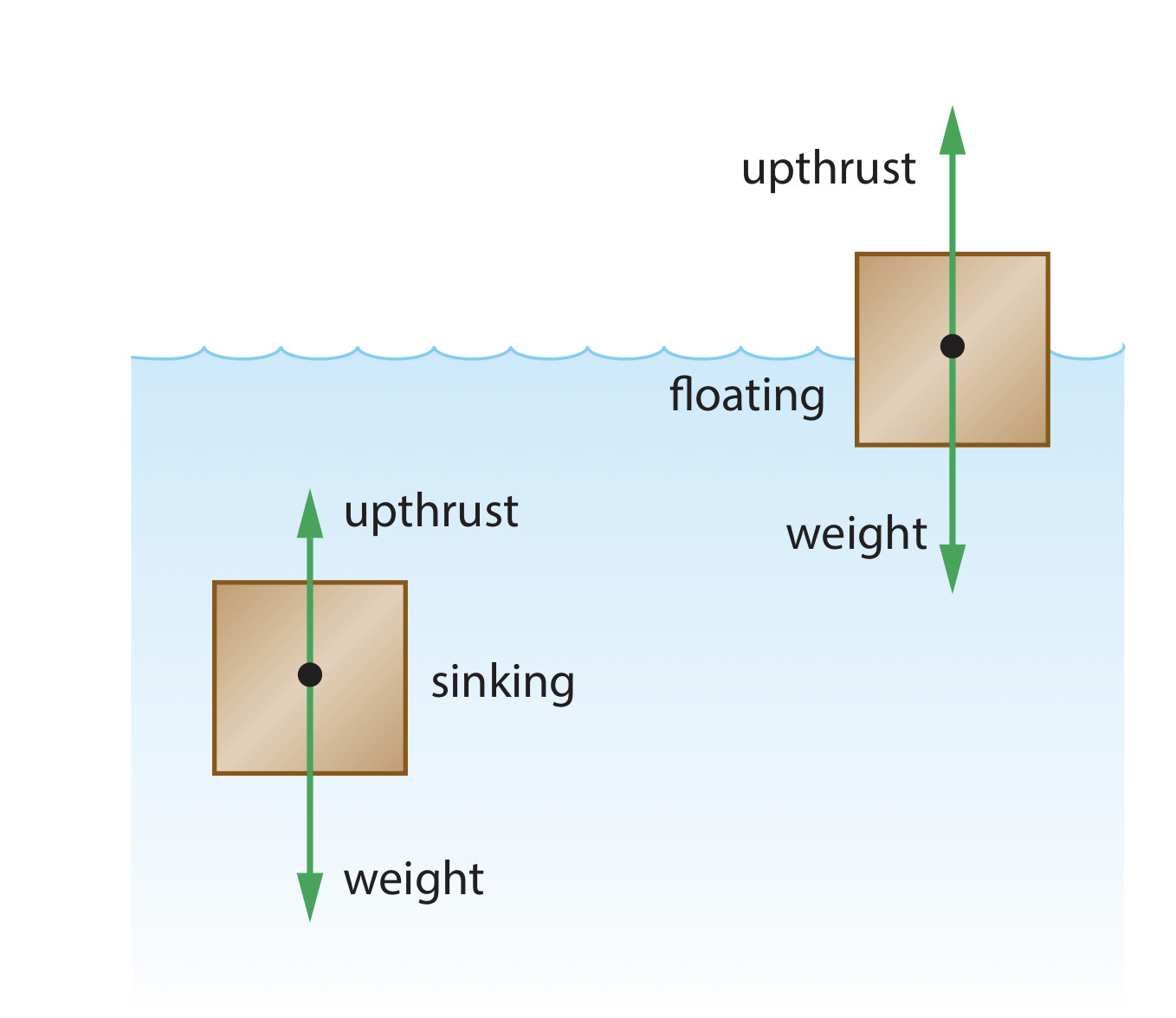
Upthrust
| upthrust |
|---|
| Any object placed in a fluid experiences an upward force which is upthrust |
 |
Frictional forces
| Frctional forces | |
|---|---|
| dynamic friction | static friction |
| ${fd}=μdR$ | ${fs}=μsR$ |
| Where f is frictional forces, μ is coefficient of dynamic friction and R is the normal reaction force between the surfaces | Where f is frictional forces, μ is coefficient of static friction and R is the normal reaction force between the surfaces |
| The force of dynamic friction dose not depend on the speed of sliding | The force of static friction depend on the speed of sliding |
| ${μs}>μd$ | |
 |
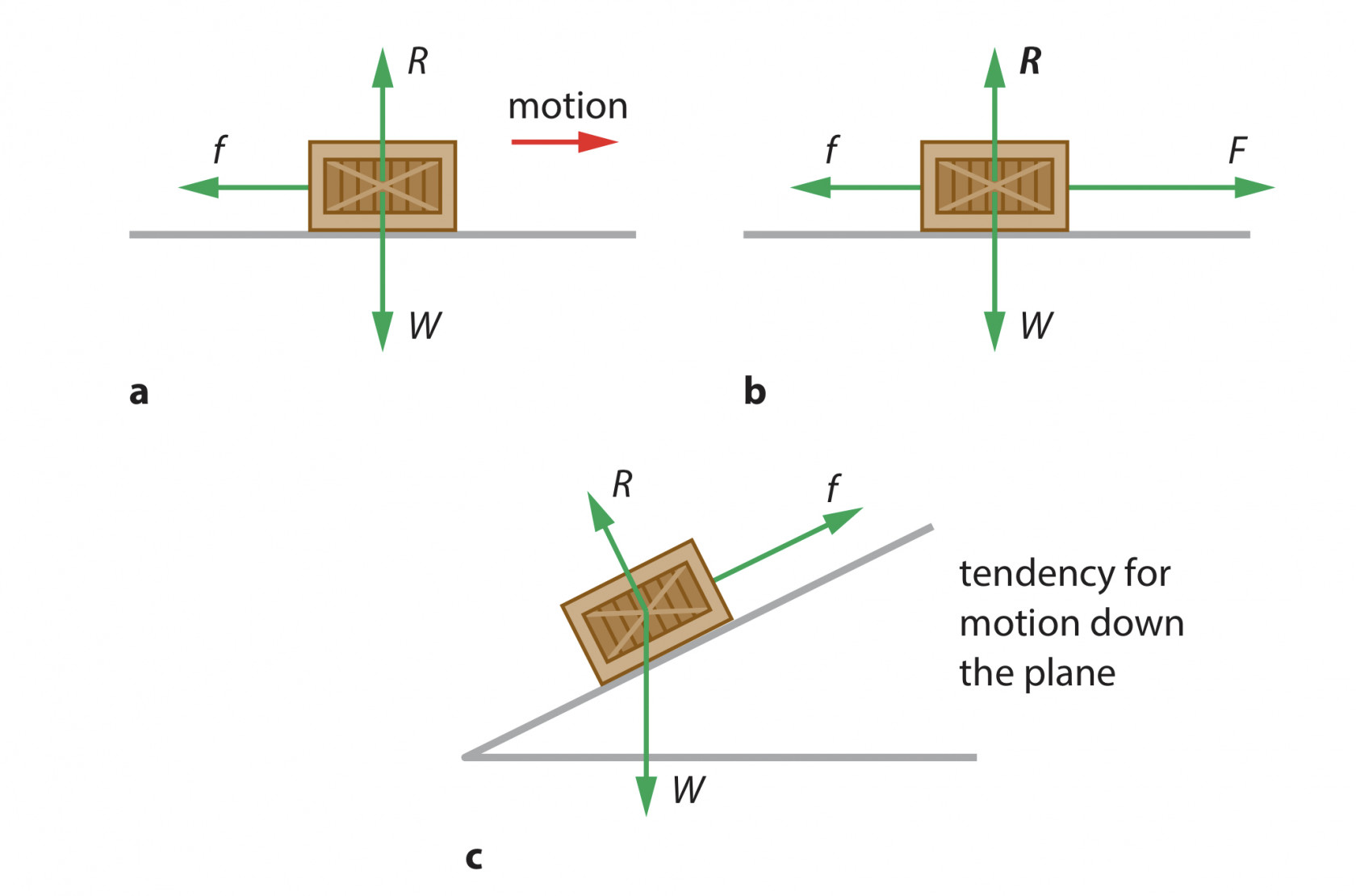
Free-body diagrams & equilibrium
Free-body diagram shows the magnitude and direction of all the forces acting on a chosen body, and in this graph we treated body as point mass (which have no volume)
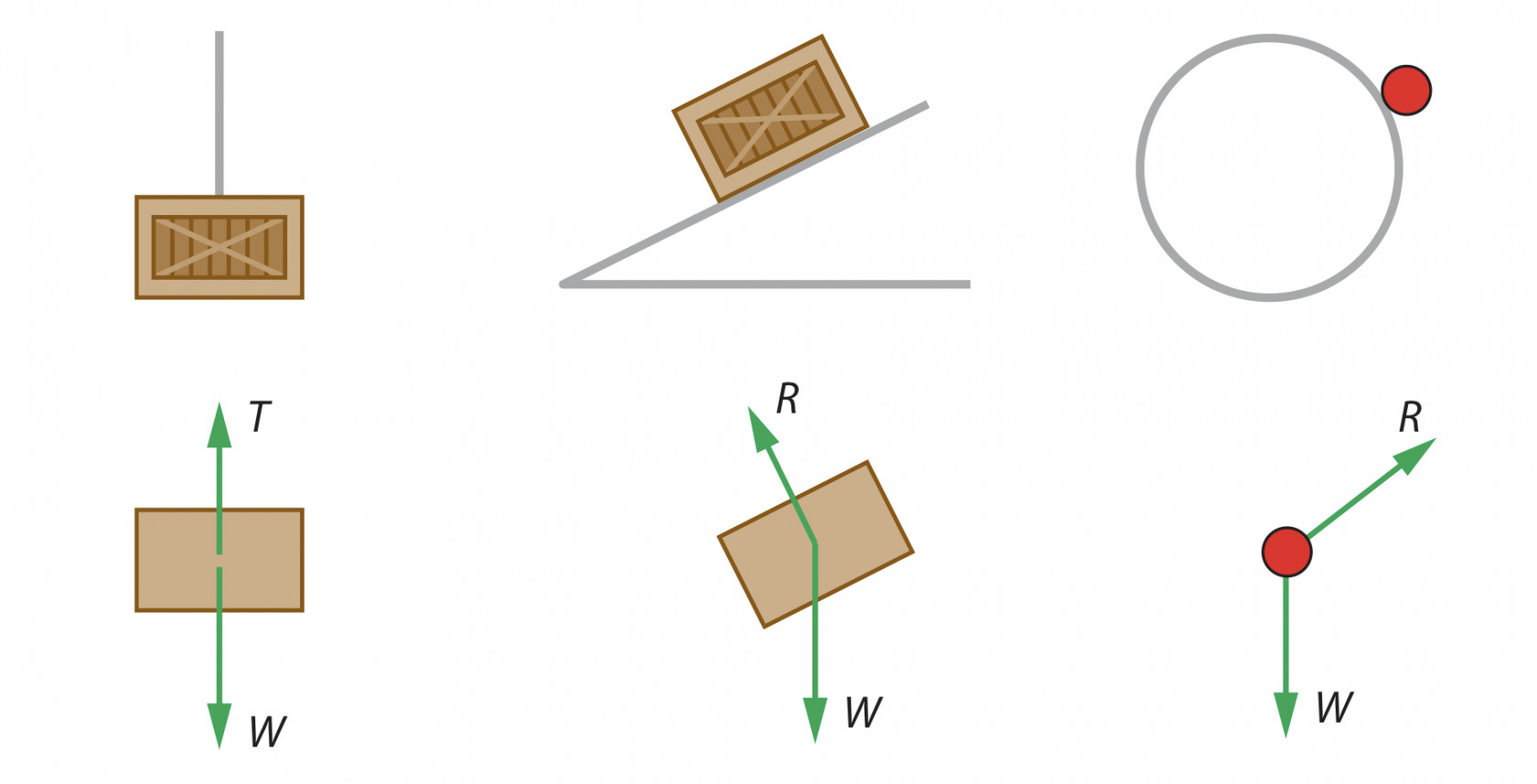Equilibrium refers to a points which net force(sum of all it's component is zero) like the situation:
· object moving in constant velocity
· object stay rest
Newton's law of motion
| Newton's first law |
|---|
| When the net force on a body is zero, the body will move with constant velocity(which may be zero) |
| Newton's third law |
|---|
| If a body A exerts a force on body B, then body B exerts a force of the same magnitude but in the opposite direction of body A. |
| Newton's second law |
|---|
| The net force on a body of constant mass is proportional to that body's acceleration and is in the same direction as the acceleration |
| F=ma(very improtant formula) |
Work, energy and power
Work done
The work done by a force is the product of the force in the direction of the displacement time and distance travel Follow the equation ${W}=Fscosθ$
Energy
Kenetic energy
$E_K=\frac{1}{2}mv^2$
$E_K$ is kenetic energy, m is mass, v is velocity of the object
Gravity potential energy
$E_P=mgh$
$E_P$ is gravity potiential energy, m is mass, h is height and g is gravity constant(9.81ms^-2^ on Earth)
Mechanical energy
$E_P=\frac{1}{2}x^2$
$E_P$ is elastic potiential energy, m is mass, x is displacement.
Power
$P=\frac{W}{t}$/$P=Fv$ Where P is power, W is work done and t is time, in the other formula, F is forces and v is velocity
Power 衡量的是规定时间内做工的能力
Efficiency
Motion
| Newton's second law in terms of momentum |
|---|
| $p=mv$ |
| $F_{net}=\frac{\Delta p}{\Delta t}$ |
| p is momentum, m is mass and v is velocity |
| The change of momentum of an object is called impulse |
| Rearranging the formula describing Newton’s second law results in the following expression |
| F~net~${\Delta t}$=$m{\Delta v}$ |
| left side is impluse and right side is change in momentum |
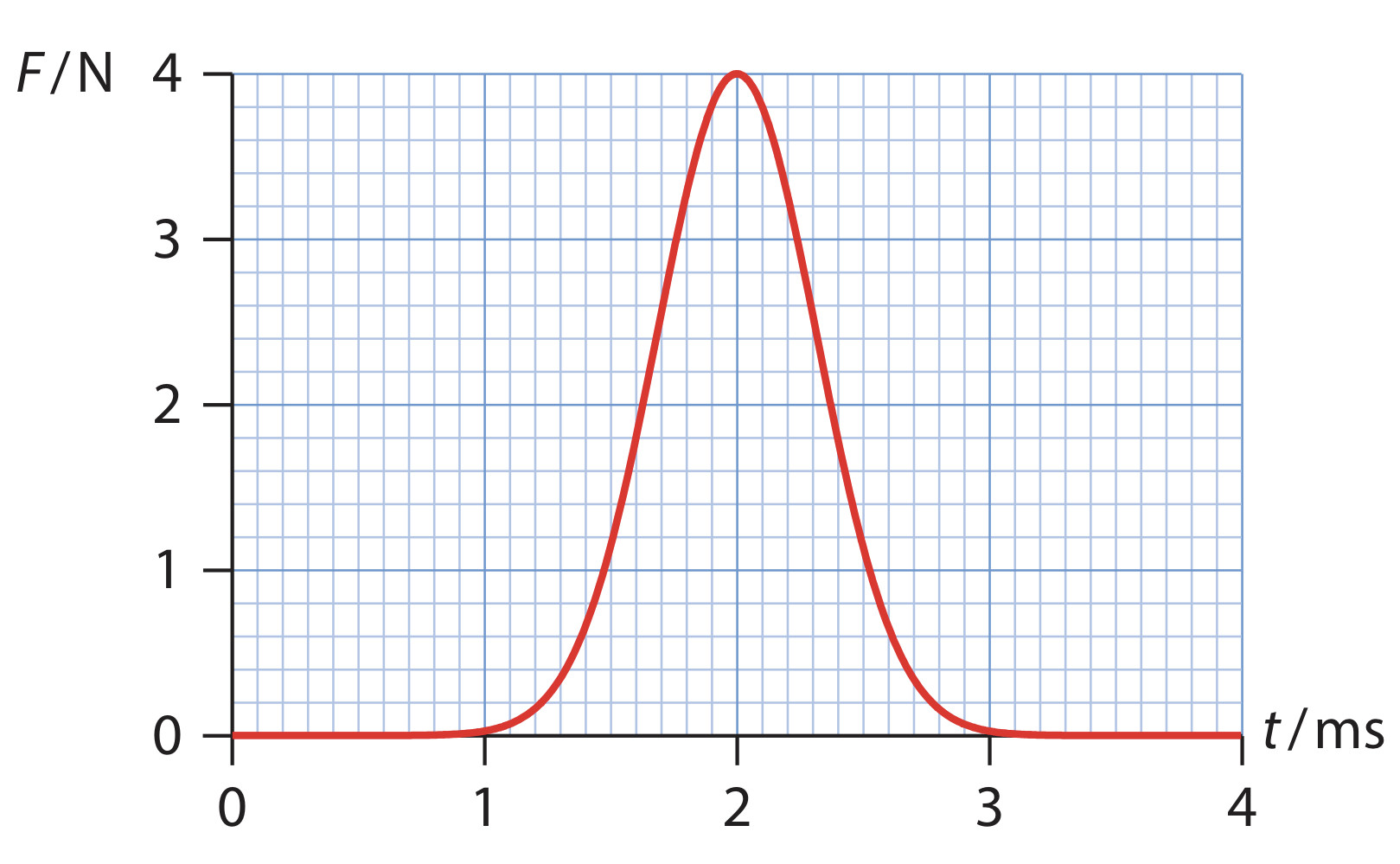
Impluse and force-time graphs
Impluse is the area in the force-time graph
conservation of momentum
When the net force on a system is zero the momentum does not change
Follow the equation: $m_1u_1+m_2u_2=m_1v_1+m_2v_2$
Where m is mass, u is initial velocity and v is final velocity